Variance Reduction Techniques

Variance Reduction Techniques are usually applied to increase precision of probabilistic estimates, such as interpolations/extrapolations off historical data. While it is very much valued in the field of datamining, when it comes to financial economics, number crunching is usually only a part of the profit-desired solution, as known and unknown risks never go away. For example, "...investment banks use very complicated Monte Carlo simulations to price esoteric mortgage-backed securities." (Wolfram)

Common Random Numbers
This is a popular method of variance reduction for simulation studies where 2+ systems are compared. The basic idea is to apply two or more configuration inputs to the tested system.

Caveat:
"
The method of common random numbers (also known as the method of correlated sampling, the method of matched pairs, or the method of matched sampling) does not always work. It can backfire if the the engineer of the Monte Carlo simulation creates a negative, rather than positive, correlation between the two random variables 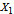and .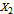
"
Source: Wolfram

Option Delta

In financial engineering, CRN are sometimes used to estimate option delta when an explicit solution isn't available. Example below:

C: value of a Call option
S: value of underlying asset
Delta:

Let epsilon: 0+, i.e. very small positive value, then the finite-difference ratio:

C(S +/- epsilon) are estimated using the same set of CRNs.

source: Variance Reduction Methods, Haugh