Option prices are more efficient than you think

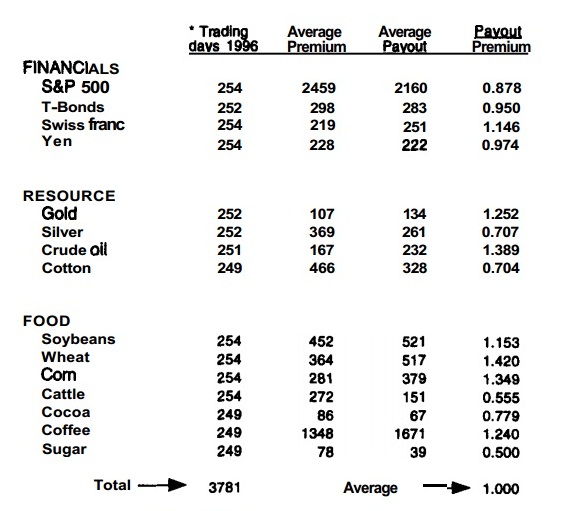
In The Options Edge, Gallagher looked at performance of (some interpolated) At-The-Money straddles between 15 futures options to determine whether options are indeed traded at a constant premium over future realized volatility, and concluded that they are most likely not.

In the experiment, he held and rolled front month straddles til expiration, back to back. In the last column, a ratio of 1 would mean the premium paid was exactly at fair value, if the ratio is below 1 the sellers made money, and vice versa.

Here are the findings:

 

We can see that at least for the year 1996, futures ATM Straddles were roughly traded at fair value.

My personal take on this

The normal distribution assumption off Black Scholes valuation is most likely off, significantly.

Empirically, blindly selling options does not generate a positive E(PnL), i.e. Expected Profit/Loss, particularly after transaction, hedging costs. At the same time, this also means buying volatility through options does not always carry a cost, this then in turn could lead to some very interesting trading strategies with very favorable risk/reward potentials.  

Respecting the proprietary trading business model

So I'm in Shanghai, heading a proprietary trading project, and I can already sense the need to replace a few of the locals in the team as they seem to have concluded this is more of a game than serious business. To make the operations profitable, every part of the business must be executed near flawlessly and on time, and we simple cannot take on the risk of second guessing little details such as "are these transaction costs in USD or RMB?"

How a lot of new guys lose money even with net profitable EV trading strategies

Once the business model is understood, a lot of the new guys assume that profits would come without much work whatsoever. From my experience, this is exactly the point where things start to go south; fat finger mistakes, miscommunications around order submissions, PnL accounting errors, violations of risk limits, etc.

Some tedious (maybe fun for others), necessary work for the trading entity

• Accurate book keeping, Mark to Market on a daily basis
• Negotiations with brokerage firms for best possible transaction costs
• Solid risk limit implementations in real time
• Daily research minimum to confirm availability of currently exploited inefficiency

 

About P&L volatility

Here I will talk about how longer term P&L (Profit & Loss) volatility affects instantaneous (shorter term) expected returns, and some practical means to apply this information.

In the Black-Scholes framework, the expected return is explained as
E(R) = (u - v^2 / 2) * (T - t)

where
E(R) = Expected return
u = expected drift, usually the risk-free interest rate
v = expected volatility of return
T = time at the end of the trade
t = time at the beginning of the trade

With basic calculus, we can see that the (u - v^2 / 2) portion is derived as an integral of v, so return volatility is important for not just risk management, but also estimating P&L.

So it looks like P&L volatility lowers longer term returns off short term P&L estimates, e.g. if a trading strategy is expected to average 1%/week, and if the P&L volatility, a random component, is expected to be greater than 0, then its expected annual return with weekly compounding would be LESS than (1.01)^52.

Assume that there is a 3% weekly volatility on an asset valued $1. We can visualize that a net loss occurs when when a 3% positive return is followed by a 3% negative move of $1.03.

See Neil A. Chriss' Black-Scholes and Beyond for more details behind the math.

Leverage
 
We can now see that applying leverage to a trading strategy does not necessarily increase expected risks more than the expected returns. This is also apparent in the performance of leveraged ETFs.

An example of exploiting this phenomenon

A theoretical inefficeincy exists if one was to sell short a leveraged ETFs/ETNs, hedged with unleveraged ETFs of identical underlyings. Of course it would still have to overcome transaction costs and product dependent limitations around shortselling.